Neural Scene Flow Prior

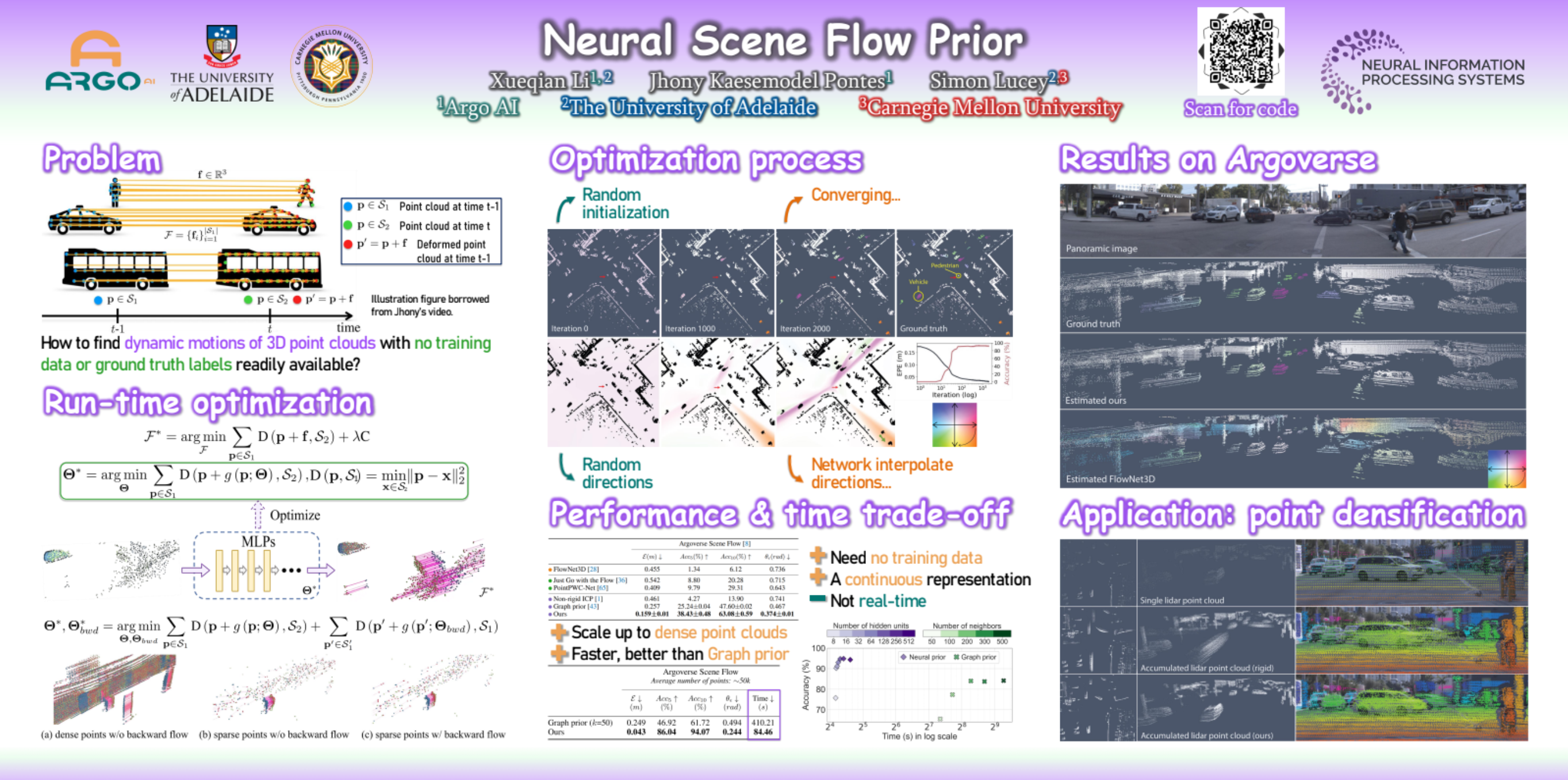
Before the deep learning revolution, many perception algorithms were based on runtime optimization in conjunction with a strong prior/regularization penalty. A prime example of this in computer vision is optical and scene flow. Supervised learning has largely displaced the need for explicit regularization. Instead, they rely on large amounts of labeled data to capture prior statistics, which are not always readily available for many problems. Although optimization is employed to learn the neural network, the weights of this network are frozen at runtime. As a result, these learning solutions are domain-specific and do not generalize well to other statistically different scenarios. This paper revisits the scene flow problem that relies predominantly on runtime optimization and strong regularization. A central innovation here is the inclusion of a neural scene flow prior, which uses the architecture of neural networks as a new type of implicit regularizer. Unlike learning-based scene flow methods, optimization occurs at runtime, and our approach needs no offline datasets—making it ideal for deployment in new environments such as autonomous driving. We show that an architecture based exclusively on multilayer perceptrons (MLPs) can be used as a scene flow prior. Our method attains competitive—if not better—results on scene flow benchmarks. Also, our neural prior’s implicit and continuous scene flow representation allows us to estimate dense long-term correspondences across a sequence of point clouds. The dense motion information is represented by scene flow fields where points can be propagated through time by integrating motion vectors. We demonstrate such a capability by accumulating a sequence of lidar point clouds.

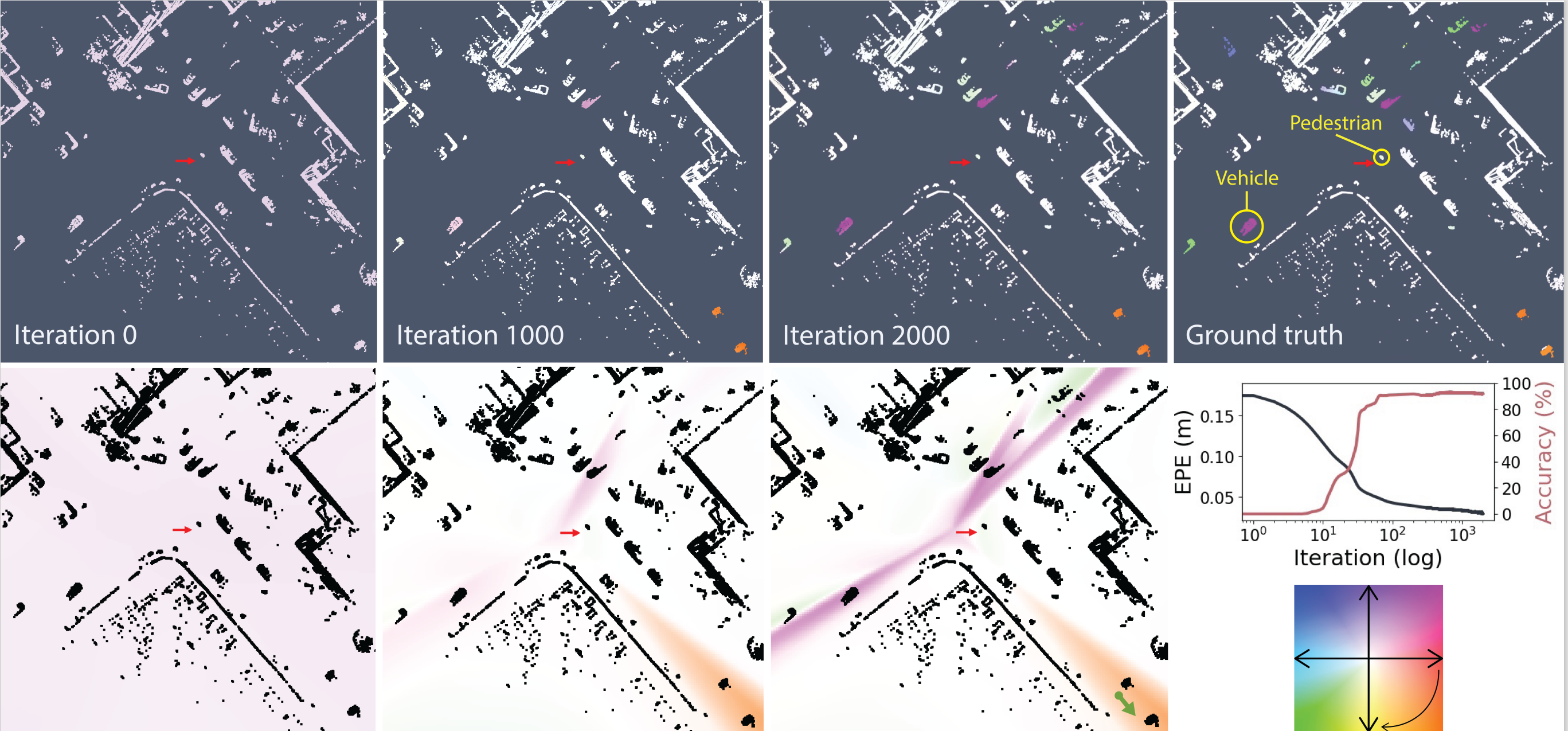
Example showing how the estimated scene flow and the continuous flow field (bottom) given by our neural prior change as the optimization converges to a solution. We show a top-view dynamic driving scene from Argoverse Scene Flow. The scene flow color encodes the magnitude (color intensity) and direction (angle) of the flow vectors. For example, the purplish vehicles are heading northeast. The red arrow shows the position and direction of travel of the autonomous vehicle, which is stopped, waiting for a pedestrian to cross the street. Note how the predicted scene flow is close to the ground truth at iteration 2k. At iteration 0, the scene flow is random, given the random initialization of the neural prior. Thus having very small magnitudes for the random directions. As the optimization went on, the flow fields became better constrained. A simple way to interpret the flow fields is to sample a point at any location in the continuous scene flow field to recover an estimated flow. For example, imagine sampling a point around the orange region in the flow field at iteration 2k (green arrow in the bottom right). The direction of the flow vector will be pointing southeast at a specific magnitude, similar to the vehicles in the orange region.

Here we demonstrate an exmaple of doing point cloud densification using our method. Given a long sequence of point sets, we first optimize to find the flow for the successive point cloud pairs using our method. Then, we use forward Euler integration to recursively densify the point clouds. The video below shows a densified point cloud sequence across 25 frames compared to the original sparse point cloud sequence. Note that we used 11 frames to do the integration.

The authors would like to thank Chen-Hsuan Lin for useful discussions through the project, review and help with section 3. We thank Haosen Xing for careful review of the entire manuscript and assistance in several parts of the paper, Jianqiao Zheng for helpful discussions. We thank all anonymous reviewers for their valuable comments and suggestions to make our paper stronger.